python draw tree from dictionary
Source code please see in Github repository
Q1.Hash Tree
We have this hash functions shown in the figure below.
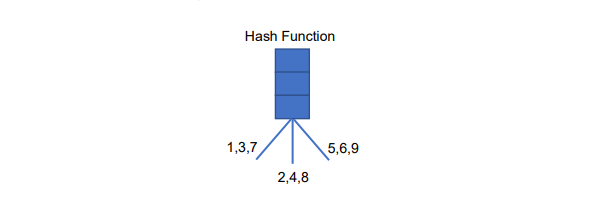
(a) Please write a program to generate a hash tree with max leaf size 3, output the nested list (or nested dict) of the hash tree hierarchically and draw the structure of the hash tree (you can write program to draw this hash tree or just manually draw it according to the nested list you output).
Build a data structure of LinkedList
In the last level of leaf node, it may exist items over 3 but the max leaf size == 3. Therefore, we could use Linkedlist to store items whose index >= 2. We first build a LinkedList structure.
class Node(object): def __init__(self, data): self.data = data self.next = None class LinkedList(object): def __init__(self): self.head = None self.tail = None # is empty => True def is_empty(self): return self.head is None # Append node in the end of Linkedlist def append(self, data): node = Node(data) if self.head is None: self.head = node self.tail = node else: self.tail.next = node self.tail = node # Traversal all elements in Linkedlist def iter(self): if not self.head: return cur = self.head yield cur.data while cur.next: cur = cur.next yield cur.data Define the Hash Tree function
import sys def divide_subnode(node, depth, max_level, max_leaf_size): """ To divide the node, recursion function :node: set of node :depth: depth of the item :max_level: the maximum level of tree :max_leaf_size: the maximum leaf size """ # If the size of node <= max_leaf_size, we don't need to split the node if len(node) <= max_leaf_size: return node # When depth == max_level, it need to be considered separately if depth == max_level: if len(node) <= max_leaf_size: return node else: # Remind the max leaf size = 3 so when depth == max_level with len(node) > 3, we need to use a kind of structure to store this node # A linked list is used to store items whose index >= 2 # structure = [item, item, LinkedList] linked_list = LinkedList() for item in node[2:]: linked_list.append(item) structure = [node[0], node[1], linked_list] # Show the linked list for node in linked_list.iter(): print(node) print() return structure # Implement the hash funtion to divide node subnode = [[],[],[]] for item in node: if item[depth] in [1, 3, 7]: subnode[0].append(item) elif item[depth] in [2, 4, 8]: subnode[1].append(item) elif item[depth] in [5, 6, 9]: subnode[2].append(item) else: # If 0 exits, the program would be terminated because we don't define Hash funtion on 0 print("Cannot apply Hash function on 0") sys.exit(1) return [divide_subnode(subnode[0], depth+1, max_level, max_leaf_size), \ divide_subnode(subnode[1], depth+1, max_level, max_leaf_size), \ divide_subnode(subnode[2], depth+1, max_level, max_leaf_size)] def create_hash_tree(input, begin_depth=0, max_level=3, max_leaf_size=3): """ Create Hash Tree :input: (list) Input a nested list as the input :begin_depth: the beginning depth, default = 0 :max_level: the maximum level of tree, default = 3 :max_leaf_size: the maximum leaf size, default = 3 :return: (list) hash_tree """ hash_tree = divide_subnode(input, begin_depth, max_level, max_leaf_size) return hash_tree # The example is 3-item so we build a hash tree with max-level 3, starting from 0 depth # Example input input = [[1,2,3],[1,3,9],[1,4,5],[1,4,6],[1,5,7],[1,5,9],[1,6,8],[1,6,9],[1,8,9], [2,3,9],[2,5,6],[2,5,7],[2,5,9],[2,6,7],[2,6,8],[2,6,9],[2,7,8],[2,7,9],[2,8,9], [3,4,6],[3,4,8],[3,7,8], [4,5,6],[4,5,8],[4,5,9],[4,7,8],[4,7,9],[4,8,9], [5,6,7],[5,6,8],[5,7,8],[5,7,9],[5,8,9], [6,7,9],[6,8,9], [7,8,9]] create_hash_tree(input, begin_depth=0, max_level=3) [1, 8, 9] [3, 4, 6] [7, 8, 9] [2, 6, 9] [4, 5, 6] [4, 5, 9] [[[[1, 3, 9], [3, 7, 8]], [[[1, 2, 3]], [[3, 4, 8]], [[1, 4, 5], [1, 4, 6], <__main__.LinkedList at 0x2b9156641d0>]], [[[1, 5, 7]], [[1, 6, 8]], [[1, 5, 9], [1, 6, 9]]]], [[[], [[2, 7, 8], [4, 7, 8]], [[2, 3, 9], [2, 7, 9], [4, 7, 9]]], [[2, 8, 9], [4, 8, 9]], [[[2, 5, 7], [2, 6, 7]], [[2, 6, 8], [4, 5, 8]], [[2, 5, 6], [2, 5, 9], <__main__.LinkedList at 0x2b915664518>]]], [[[5, 7, 8], [5, 7, 9], [6, 7, 9]], [[5, 8, 9], [6, 8, 9]], [[5, 6, 7], [5, 6, 8]]]] Therefore, we can draw the hash tree below
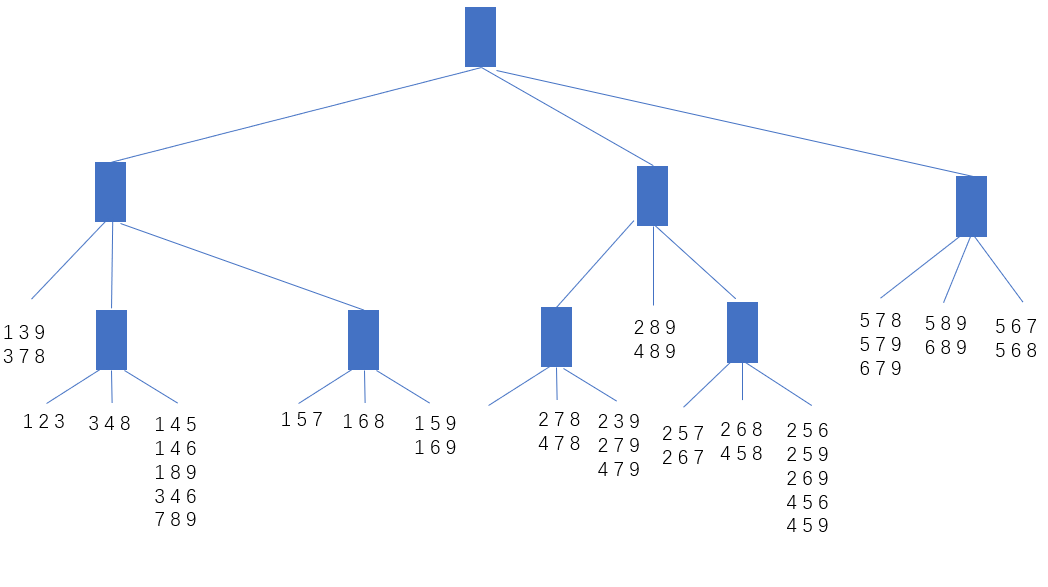
(b) Given a transaction that contains items {1, 3, 5, 6, 7, 9}, how many comparisons are needed using the hash tree which you generate above? Please circle these candidates in the hash tree. No programming required.
Match transaction 10 candidates in the hash tree which are circled. It needs to compare totally 34 times using my generated hash tree.
1 + 35679 13 + 5679 2+2+2+1=7 15 + 679 2+1+1=4 16 + 79 1+2=3 17 + 9 2 3 + 5679 35 + 679 2+1+2=5 36 + 79 1+2=3 37 + 9 2 5 + 679 56 + 79 1+2=3 57 + 9 2 679 3 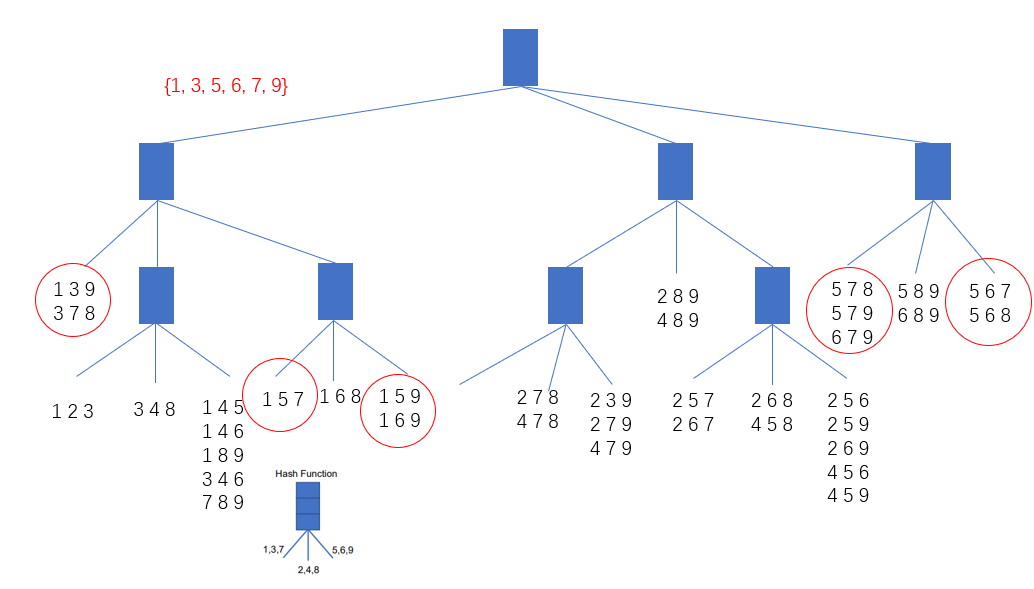
Q2. FP-Tree
Suppose you are given some transactions and a vocabulary that map terms to indexes. Please use
FP-Tree algorithm to discover the frequent itemsets.
Data Description:
- topi-i.txt
Input file of frequent pattern mining algorithms. Each line represents a transaction with indices of terms.
format: term1_index term2_index term3_index ...
Columns are separated by a space.
- vocab.txt
Dictionary that maps term index to term.
format: term_index term
Columns are separated by a space.
- pattern-i.txt:
The file you need to submit, which contains your result for this frequent pattern mining task. Each line represents a transaction with frequent itemsets sorted in descending order of support count.
format: support_count term1 term2 ...
support_count and term1 are separated by a tab, while terms are separated by a space.
Here we give an example:
233 rule association 230 random 227 finding 203 mining pattern Questions:
(a) Please write a program to implement FP-growth algorithm and find all frequent itemsets with support >= 400 in the given dataset.
(b) Based on the result of (a), please print out those FP-conditional trees whose height is larger than 1.

Define preprocessed funtion
-
read_file()function that converts txt into nested list -
create_init_set()function that generates transaction dictionary which is as initial data to inputcreate_fp_tree()function
def read_file(file): """ Read files from txt """ items_bought = [] # origin data with open(file,"r") as f: for line in f.readlines(): items_bought.append(line.strip().split()) return items_bought def create_init_set(items_bought): trans_dict={} for trans in items_bought: key = frozenset(trans) if key not in trans_dict: trans_dict[key] = 1 else: trans_dict[key] += 1 return trans_dict Define the class of TreeNode and make a vocab dict
# Define the vocab_dict which is used to transform index to vocabulary vocab_dict = {} with open("vocab.txt", 'r') as f: for line in f.readlines(): term = line.strip().split("\t") vocab_dict[term[0]] = term[1] # Define the structure of TreeNode class TreeNode: def __init__(self, name_value, num_occur, parent_node): self.name = name_value self.node_link = None self.count = num_occur self.parent = parent_node self.children = {} # Add the count of node def inc(self, num_occur): self.count += num_occur # Print tree's structrue in the terminal def display(self, index=1): print(' '*index, self.name, ' ', self.count) for child in self.children.values(): child.display(index+1) # Calculate the height of tree def get_height(self, index=1): mid = 0 for child in self.children.values(): if child.get_height(index+1) >= mid: mid = child.get_height(index+1) return max(index, mid) # Transform tree to a nested list # According to the output EXAMPLE => [parent, children] def transform_to_list(self): if self.name in vocab_dict: node_info = vocab_dict[self.name] + " " + str(self.count) else: node_info = self.name + " " + str(self.count) if len(self.children) == 0: return node_info local_list = [] for child in self.children.values(): local_list.append(child.transform_to_list()) return [node_info, local_list] Define FP-growth function
def update_header(node_to_test, target_node): """ Update header table :node_to_test: the entry of the node :target_node: Target node to link """ # To find the node with node_link == None while node_to_test.node_link != None: node_to_test = node_to_test.node_link # Link the target_node on node node_to_test.node_link = target_node def update_fp_tree(items, fp_tree, header_table, count): """ Update FP Tree :items: items in frequent itemsets :fp_tree: TreeNode :header_table: header table :count: added count """ if items[0] in fp_tree.children: # If items[0] is as child node, fp_tree.count += count fp_tree.children[items[0]].inc(count) else: # If items[0] is not a child node, create a new branch fp_tree.children[items[0]] = TreeNode(items[0], count, fp_tree) # Update linked list of the frequent itemsets if header_table[items[0]][1] == None: header_table[items[0]][1] = fp_tree.children[items[0]] else: update_header(header_table[items[0]][1], fp_tree.children[items[0]]) # Recursion if len(items) > 1: update_fp_tree(items[1::], fp_tree.children[items[0]], header_table, count) def create_fp_tree(trans_dict, threshold=400): """ Create FP Tree :trans_dict: transaction dictionary :threshold: bound that decides whether to remove the item in transactions. Default value = 400 :return: fp_tree, header_table, filtered_trans_dict """ header_table = {} # First Scan: Construct the header table and sort it for items in trans_dict: for item in items: header_table[item] = header_table.get(item, 0) + trans_dict[items] # Delete the elements with frequency < threshold for k in set(header_table.keys()): if header_table[k] < threshold: del(header_table[k]) # Sort the header table by descending frequency header_table = dict(sorted(header_table.items(), key=lambda p:p[1], reverse=True)) # Frequent itemsets contain items whose frequency >= threshold freq_itemsets = set(header_table.keys()) if len(freq_itemsets) == 0: return None, None, None for k in header_table: header_table[k] = [header_table[k], None] # Initialize the FP Tree with root node fp_tree = TreeNode('Null Set', 1, None) # Second Scan: remove the infrequent item in transaction and sort it filtered_trans_dict = {} for trans, count in trans_dict.items(): local_dict = {} for item in trans: if item in freq_itemsets: local_dict[item] = header_table[item][0] if len(local_dict) > 0: # Sorted transaction item by descending frequency ordered_items = [x[0] for x in sorted(local_dict.items(), key=lambda p:p[1], reverse=True)] # Build the filtered transaction dictionary key = frozenset(ordered_items) if key not in filtered_trans_dict: filtered_trans_dict[key] = count else: filtered_trans_dict[key] += count # Update FP Tree using ordered items update_fp_tree(ordered_items, fp_tree, header_table, count) # Sort the filtered transaction dictionary as an output filtered_trans_dict = dict(sorted(filtered_trans_dict.items(), key=lambda p:p[1], reverse=True)) return fp_tree, header_table, filtered_trans_dict Generate FP-Tree from txt file
# Test for topic-0.txt items_bought = read_file("topic-0.txt") trans_dict = create_init_set(items_bought) fp_tree, header_table, filtered_trans_dict = create_fp_tree(trans_dict, threshold=400) # fp_tree.display() print(filtered_trans_dict) header_table {frozenset({'248'}): 668, frozenset({'390'}): 624, frozenset({'458'}): 500, frozenset({'298'}): 328, frozenset({'382'}): 324, frozenset({'118'}): 303, frozenset({'390', '382'}): 296, frozenset({'473'}): 217, frozenset({'723'}): 208, frozenset({'225'}): 170, frozenset({'382', '723'}): 123, frozenset({'382', '225'}): 108, frozenset({'473', '248'}): 67, frozenset({'458', '248'}): 52, frozenset({'298', '248'}): 47, frozenset({'390', '248'}): 45, frozenset({'390', '298'}): 38, frozenset({'473', '390'}): 37, frozenset({'118', '248'}): 37, frozenset({'382', '458'}): 33, frozenset({'382', '248'}): 28, frozenset({'118', '390'}): 26, frozenset({'225', '248'}): 23, frozenset({'390', '458'}): 23, frozenset({'390', '225'}): 23, frozenset({'390', '723'}): 23, frozenset({'390', '382', '723'}): 23, frozenset({'298', '458'}): 21, frozenset({'390', '382', '248'}): 20, frozenset({'390', '382', '298'}): 20, frozenset({'118', '723'}): 20, frozenset({'723', '298'}): 18, frozenset({'118', '458'}): 18, frozenset({'473', '382'}): 18, frozenset({'390', '382', '225'}): 15, frozenset({'382', '225', '248'}): 14, frozenset({'473', '118'}): 13, frozenset({'118', '298'}): 13, frozenset({'473', '382', '723'}): 12, frozenset({'118', '390', '382'}): 12, frozenset({'473', '723'}): 11, frozenset({'473', '225'}): 11, frozenset({'382', '723', '458'}): 11, frozenset({'382', '298'}): 11, frozenset({'473', '298'}): 9, frozenset({'458', '298', '248'}): 9, frozenset({'473', '458'}): 9, frozenset({'473', '390', '382'}): 9, frozenset({'225', '298'}): 9, frozenset({'118', '382'}): 9, frozenset({'723', '458'}): 9, frozenset({'473', '382', '225'}): 8, frozenset({'473', '118', '248'}): 8, frozenset({'118', '382', '723'}): 7, frozenset({'723', '248'}): 7, frozenset({'382', '723', '248'}): 7, frozenset({'458', '473', '248'}): 7, frozenset({'473', '390', '248'}): 6, frozenset({'382', '723', '298'}): 6, frozenset({'473', '382', '248'}): 5, frozenset({'118', '225'}): 5, frozenset({'118', '390', '723'}): 4, frozenset({'473', '390', '298'}): 4, frozenset({'390', '382', '458'}): 4, frozenset({'225', '723'}): 4, frozenset({'390', '382', '225', '248'}): 4, frozenset({'473', '118', '390'}): 3, frozenset({'118', '382', '458'}): 3, frozenset({'390', '382', '723', '298'}): 3, frozenset({'118', '382', '225'}): 3, frozenset({'473', '298', '458'}): 2, frozenset({'118', '390', '248'}): 2, frozenset({'458', '473', '723', '248'}): 2, frozenset({'382', '225', '298'}): 2, frozenset({'473', '118', '382'}): 2, frozenset({'390', '225', '248'}): 2, frozenset({'390', '723', '458'}): 2, frozenset({'473', '118', '382', '723'}): 2, frozenset({'473', '382', '225', '248'}): 2, frozenset({'473', '390', '382', '723'}): 2, frozenset({'118', '298', '458'}): 2, frozenset({'473', '390', '382', '225'}): 1, frozenset({'473', '723', '298'}): 1, frozenset({'473', '390', '225', '723'}): 1, frozenset({'225', '458'}): 1, frozenset({'118', '382', '248'}): 1, frozenset({'118', '723', '458'}): 1, frozenset({'473', '118', '298'}): 1, frozenset({'118', '390', '298'}): 1, frozenset({'473', '382', '723', '298'}): 1, frozenset({'118', '723', '248'}): 1, frozenset({'390', '723', '298'}): 1, frozenset({'298', '382', '248'}): 1, frozenset({'473', '225', '248'}): 1, frozenset({'225', '382', '723'}): 1, frozenset({'298', '382', '458'}): 1, frozenset({'473', '382', '723', '248'}): 1, frozenset({'225', '382', '723', '298'}): 1, frozenset({'473', '382', '298'}): 1, frozenset({'298', '390', '248'}): 1, frozenset({'118', '225', '248'}): 1, frozenset({'118', '298', '723', '248'}): 1, frozenset({'458', '225', '248'}): 1, frozenset({'390', '723', '248'}): 1, frozenset({'118', '390', '458'}): 1, frozenset({'118', '390', '225'}): 1, frozenset({'382', '248', '723', '473', '390'}): 1, frozenset({'473', '382', '723', '458'}): 1, frozenset({'118', '390', '382', '723'}): 1, frozenset({'225', '723', '298'}): 1, frozenset({'458', '390', '382', '248'}): 1, frozenset({'225', '723', '248'}): 1, frozenset({'473', '390', '723'}): 1, frozenset({'298', '390', '473', '248'}): 1, frozenset({'473', '118', '390', '723'}): 1, frozenset({'458', '118', '248'}): 1, frozenset({'473', '118', '723', '248'}): 1, frozenset({'473', '390', '382', '248'}): 1, frozenset({'473', '118', '723'}): 1, frozenset({'473', '118', '225'}): 1, frozenset({'118', '298', '248'}): 1, frozenset({'390', '225', '458'}): 1, frozenset({'458', '382', '248'}): 1, frozenset({'458', '390', '248'}): 1, frozenset({'298', '723', '248'}): 1, frozenset({'473', '382', '458'}): 1, frozenset({'458', '473', '382', '248'}): 1, frozenset({'473', '723', '248'}): 1, frozenset({'118', '723', '298'}): 1, frozenset({'473', '298', '248'}): 1, frozenset({'298', '248', '723', '473', '390'}): 1} {'390': [1288, <__main__.TreeNode at 0x2b915671518>], '382': [1163, <__main__.TreeNode at 0x2b915671320>], '248': [1087, <__main__.TreeNode at 0x2b915671278>], '458': [720, <__main__.TreeNode at 0x2b915671630>], '298': [560, <__main__.TreeNode at 0x2b915671588>], '723': [528, <__main__.TreeNode at 0x2b9156715f8>], '118': [509, <__main__.TreeNode at 0x2b915671208>], '473': [488, <__main__.TreeNode at 0x2b915671550>], '225': [416, <__main__.TreeNode at 0x2b915671400>]} Begin to Mine FP-tree
To mine the FP-tree, we need to start from certain node and go through all nodes in the direction of root and build conditional pattern base. Then using the pattern base to generate FP-conditional tree. Finally, through recursively mining FP-conditional tree, we can gain the frequent itemsets pattern.
# Ascend FP Tree def ascend_fp_tree(leaf_node, prefix_path): if leaf_node.parent != None: prefix_path.append(leaf_node.name) ascend_fp_tree(leaf_node.parent, prefix_path) # Find FP-conditional base def find_cond_pat_base(base_pat, header_table): tree_node = header_table[base_pat][1] cond_pats = {} while tree_node != None: prefix_path = [] ascend_fp_tree(tree_node, prefix_path) if len(prefix_path) > 1: cond_pats[frozenset(prefix_path[1:])] = tree_node.count tree_node = tree_node.node_link return cond_pats def mine_fp_tree(in_tree, header_table, threshold, pre_fix, freq_item_list, min_height): """ Mine the frequent pattern itemsets from FP-tree :in_tree: not used :threshold: The minimum support :pre_fix: the frequent items set in the last recursion :freq_item_list: final frequent items pattern to output :min_height: The min height of conditional FP-tree to print """ items_list = [(v[0], v[1][0]) for v in sorted(header_table.items(), key=lambda p:p[1][0])] # Notice a bug p[1][0] is True, p[0] is false for item, count in items_list: new_freq_set = pre_fix.copy() new_freq_set.add(vocab_dict[item]) freq_item_list.append([count, new_freq_set]) # Construct conditional pattern base cond_pattern_base = find_cond_pat_base(item, header_table) # print(cond_pattern_base) # Build conditional FP trees cond_tree, cond_header_table, _ = create_fp_tree(cond_pattern_base, threshold) # If FP-conditional tree exists if cond_tree: # Find FP-conditional tree whose height is larger than 1 if cond_tree.get_height() > min_height: print("height = " + str(cond_tree.get_height())) print("list form of cond tree:") print(cond_tree.transform_to_list()) print("display cond tree") cond_tree.display() # If header_table exists if cond_header_table: mine_fp_tree(cond_tree, cond_header_table, threshold, new_freq_set, freq_item_list, min_height) def mine_from_txt(topic_file, pattern_file, threshold=400, min_height=1): """ Mine frequent itemsets pattern from topic file :topic_file: (string) the path of topic file :pattern_file: (string) the path to store the pattern file :threshold: the minimum support :min_height: the minimum height of FP-conditional tree to print """ items_bought = read_file(topic_file) # Read topic.txt file to initialize dataset => nested list trans_dict = create_init_set(items_bought) # list => transaction dict fp_tree, header_table, _ = create_fp_tree(trans_dict, threshold) # Create FP-tree and header table freq_items = [] # frequent items pattern list mine_fp_tree(fp_tree, header_table, threshold, set([]), freq_items, min_height) # Sort freq_items by descending supported count freq_items = sorted(freq_items, key=lambda p:p[0], reverse=True) print("frequent items pattern:") print(freq_items) # Write the pattern in txt file with open(pattern_file, "w") as f: for count, vocabs in freq_items: f.write(str(count) + "\t") i = 0 length = len(vocabs) for vocab in vocabs: i += 1 # Replace index with terms in vocab.txt f.write(vocab) if i < length: f.write(" ") f.write("\n") Print the FP-conditional tree and write pattern in file
According to the question description, for eache topic, we need to output to a pattern.txt file and we also need to find out FP-conditional tree with height more than 1. Therefore we do this:
# Process all topic files for i in range(5): topic_file = "topic-" + str(i) + ".txt" pattern_file = "pattern-" + str(i) + ".txt" print("processing " + topic_file) mine_from_txt(topic_file, pattern_file, threshold=400, min_height=1) print("write the pattern in " + pattern_file) print() processing topic-0.txt height = 2 list form of cond tree: ['Null Set 1', ['data 413']] display cond tree Null Set 1 390 413 frequent items pattern: [[1288, {'data'}], [1163, {'mining'}], [1087, {'algorithm'}], [720, {'graph'}], [560, {'time'}], [528, {'pattern'}], [509, {'tree'}], [488, {'efficient'}], [416, {'rule'}], [413, {'mining', 'data'}]] write the pattern in pattern-0.txt processing topic-1.txt frequent items pattern: [[1488, {'learning'}], [1050, {'using'}], [819, {'model'}], [715, {'based'}], [582, {'classification'}], [488, {'feature'}], [474, {'clustering'}], [463, {'network'}]] write the pattern in pattern-1.txt processing topic-2.txt height = 2 list form of cond tree: ['Null Set 1', ['information 475']] display cond tree Null Set 1 190 475 frequent items pattern: [[1226, {'web'}], [1211, {'information'}], [1114, {'retrieval'}], [863, {'based'}], [757, {'system'}], [707, {'search'}], [564, {'document'}], [490, {'language'}], [475, {'information', 'retrieval'}], [421, {'model'}], [414, {'semantic'}]] write the pattern in pattern-2.txt processing topic-3.txt frequent items pattern: [[1074, {'database'}], [928, {'system'}], [743, {'knowledge'}], [558, {'learning'}], [514, {'data'}], [506, {'logic'}], [493, {'reasoning'}], [446, {'model'}], [426, {'constraint'}]] write the pattern in pattern-3.txt processing topic-4.txt frequent items pattern: [[1713, {'query'}], [1163, {'database'}], [1040, {'data'}], [767, {'system'}], [637, {'processing'}], [567, {'distributed'}], [528, {'object'}], [508, {'efficient'}], [458, {'xml'}]] write the pattern in pattern-4.txt 本文链接:http://www.yelbee.top/index.php/archives/166/
velezwhinunatined.blogspot.com
Source: http://www.yelbee.top/index.php/archives/166/
0 Response to "python draw tree from dictionary"
Publicar un comentario